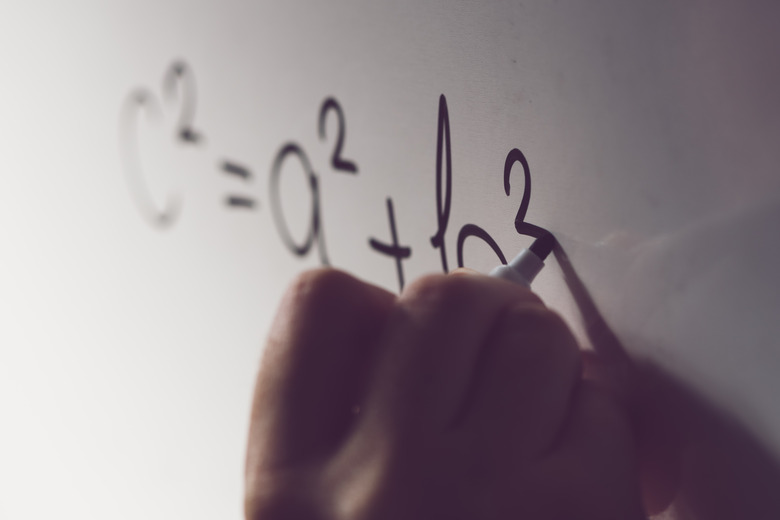How To Make A Spiral From The Pythagorean Theorem

One of geometry's virtues, from a teacher's perspective, is that it's highly visual. For example, you can take the Pythagorean Theorem – a fundamental building block of geometry – and apply it to construct a snail-like spiral with a number of interesting properties. Sometimes called a square root spiral or Theodorus spiral, this deceptively easy craft demonstrates mathematical relationships in an eye-catching way.

Pythagoras' theorem states that in a right-angle triangle, the square of the hypotenuse is equal to the square of the other two sides. Expressed mathematically, that means A squared + B squared = C squared. As long as you know the values for any two sides of a right triangle, you can use this calculation to arrive at a value for the third side. The actual unit of measurement you choose to use could be anything from inches to miles, but the relationship remains the same. That's important to remember because you won't always necessarily work with a specific physical measurement. You can define a line of any length as "1" for calculation purposes and then express every other line by its relationship to your chosen unit. That's how the spiral works.

To construct a spiral, make a right angle with sides A and B of equal length, which becomes the "1" value. Next, make another right triangle using side C of your first triangle – the hypotenuse – as side A of the new triangle. Keep side B the same length at your chosen value of 1. Repeat the same process again, using the hypotenuse of the second triangle as the first side of the new triangle. It takes 16 triangles to come all the way around to the point where the spiral would begin to overlap your starting point, which is where ancient mathematician Theodorus stopped.

The Pythagorean theorem tells us that the hypotenuse of the first triangle must be the square root of 2, because each side has a value of 1 and 1 squared is still 1. Therefore each side has an area of 1 squared, and when those are added, the result is 2 squared. What makes the spiral interesting is that the hypotenuse of the next triangle is the square root of 3, and the one after that is the square root of 4, and so on. This is why it's often referred to as a square root spiral, rather than a Pythagorean spiral or Theodorus spiral. On a practical note, if you're planning to create a spiral by drawing on paper or by cutting paper triangles and mounting them to a cardboard backing, you can calculate ahead of time how large your value of 1 can be if the finished spiral is to fit on the page. Your longest line will be the square root of 17, for whichever value of 1 you've chosen. You can work backward from the size of your page to find a suitable value of 1.

The spiral has a number of uses in classroom or tutoring settings, depending on the age of the students and their familiarity with the fundamentals of geometry. If you're just introducing the basic concepts, creating the spiral is a useful tutorial on Pythagoras' theorem. For example, you might have them do the calculations based on a value of 1 and then again using a real-world length in inches or centimeters. The spiral's resemblance to a snail shell provides an opportunity to discuss the ways mathematical relationships show up in the natural world, and – for younger kids – lends itself to colorful decorative schemes. For advanced students, the spiral demonstrates a number of intriguing relationships as it continues through multiple windings.