Tension (Physics): Definition, Formula, How To Find (W/ Diagrams & Examples)
Despite the name, the physics of tension should not cause headaches for physics students. This common type of force is found in any real-world application where a rope or ropelike object is being pulled taut.
Physics Definition of Tension
Physics Definition of Tension
Tension is a contact force transmitted through a rope, string, wire or something similar when forces on opposite ends are pulling on it.
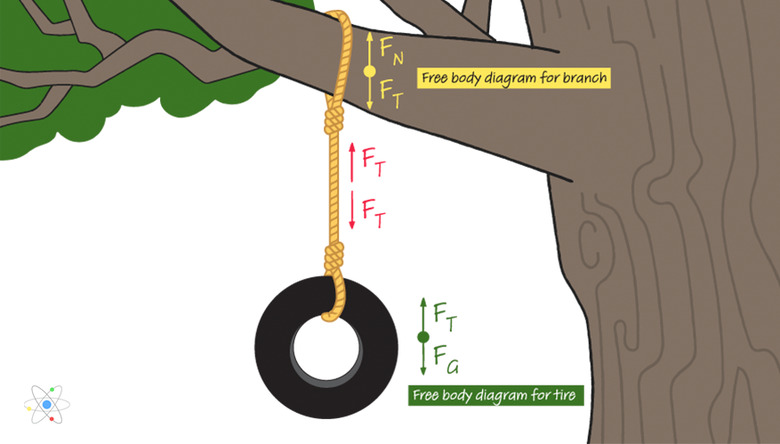
For example, a tire swing hanging from a tree causes tension in the rope holding it to the branch. The pull on the bottom of the rope comes from gravity, while the upwards pull is from the branch resisting the rope's tug.
The force of tension is along the length of the rope, and it acts equally on objects at both ends – the tire and the branch. On the tire, the force of tension is directed upwards (because tension in the rope is holding the tire up) while on the branch, the force of tension is directed downwards (the tightened rope is pulling down on the branch).
How to Find the Force of Tension
How to Find the Force of Tension
To find the force of tension on an object, draw a free-body diagram to see where this force must apply (anywhere a rope or string is being pulled taught). Then find the net force to quantify it.
Note that tension is only a pulling force. Pushing on one end of a slack rope doesn't cause any tension. Therefore, the force of tension in a free-body diagram should always be drawn in the direction that the string is pulling on the object.
In the tire-swing scenario as mentioned previously, if the tire is still – that is, not accelerating upwards or downwards – there must be a net force of zero. Since the only two forces acting on the tire are gravity and tension acting in opposite directions, those two forces must be equal.
Mathematically: Fg = Ft where _Fg_ is the force of gravity, and _Ft_ is the force of tension, both in newtons.
Recall that the force of gravity, _Fg_, is equal to an object's mass times the acceleration due to gravity g. So Fg = mg = Ft.
For a 10-kg tire, the force of tension would thus be _Ft _= 10 kg × 9.8 m/s2 = 98 N.
In the same scenario, where the rope connects with the tree branch there is also zero net force. At this end of the rope, however, the force of tension in the free-body diagram is directed downwards. However, the magnitude of the force of tension is the same: 98 N.
From this, the upwards contact force that the branch is applying on the rope must be the same as the force of tension downwards, which was the same as the force of gravity acting downwards on the tire: 98 N.
Force of Tension in Pulley Systems
Force of Tension in Pulley Systems
A common category of physics problem involving tension involves a pulley system. A pulley is a circular device that spins to let out a rope or string.
Usually high school physics problems treat pulleys as massless and frictionless, though in the real world this is never true. The mass of the rope typically gets ignored as well.
Pulley Example
Pulley Example
Suppose a mass on a table is connected by a string that bends 90 degrees over a pulley at the edge of the table and connects to a hanging mass. Assume the mass on the table has a weight of 8 N and the hanging block on the right has a weight of 5 N. What is the acceleration of both blocks?
To solve this, draw separate free-body diagrams for each block. Then find the net force on each block and use Newton's second law (_Fnet = ma_) to relate it to acceleration. (Note: the subscripts "1" and "2" below are for "left" and "right," respectively.)
Mass on the table:
The normal force and the force of gravity (weight) of the block are balanced, so the net force is all from the tension directed to the right.
\(F_{net,1}=F_{t1}=m_1a\)
Hanging mass:
On the right, tension pulls the block upwards while gravity pulls it downwards, so the net force must be the difference between them.
\(F_{net,2}=F_{t2}-m_2g=-m_2a\)
Note that the negatives in the previous equation denote that down is negative in this frame of reference and that the final acceleration of the block (the net force) is directed downwards.
Then, because the blocks are held by the same rope, they experience the same magnitude of the force of tension |Ft1| = |Ft2|. Additionally, the blocks will accelerate at the same rate, though the directions are different, so in either equation a is the same.
Using these facts and combining the final equations for both blocks:
\(a=\frac{m_2}{m_1+m_2}g=\frac{5}{8+5}(9.8)=3.77\text{m/s}^2\)
Force of Tension in Two Dimensions
Force of Tension in Two Dimensions
Consider a hanging pot rack. There are two ropes holding up a 30-kg rack, each at an angle of 15 degrees from the corners of the rack.
To find the tension in either rope, the net force in both the x- and y-directions must be balanced.
Start with the free-body diagram for the pot rack.
Of the three forces on the rack, the force of gravity is known, and it must be balanced equally in the vertical direction by both of the vertical components of the forces of tension.
\(F_g=mg=F_{T1,y}+F_{T2,y}\)
and because _FT1,y= FT2,y_ :
\(30\times 9.8 = 2 F_{T1,y}\implies F_{T1,y}=147\text{ N}\)
In other words, each rope exerts a force of 147 N upwards on the hanging pot rack.
To get from here to the total force of tension in each rope, use trigonometry.
The trigonometric relationship of sine relates the y-component, the angle and the unknown diagonal force of tension along the rope on either side. Solving for the tension on the left:
\(\sin{15}=\frac{147}{F_{T1}}\implies F_{T1}=\frac{147}{\sin{15}}=568\text{ N}\)
This magnitude would be the same on the right hand side as well, though the direction of that force of tension is different.
What about the horizontal forces each rope exerts?
The trigonometric relationship of tangent relates the unknown x-component to the known y-component and the angle. Solving for the x-component:
\(\tan{15}=\frac{147}{F_{T1,x}}\implies F_{T1,x}=\frac{147}{\tan{15}}=548.6\text{ N}\)
Because the horizontal forces are also balanced, this must be the same magnitude of force exerted by the rope on the right, in the opposite direction.
Cite This Article
MLA
Dusto, Amy. "Tension (Physics): Definition, Formula, How To Find (W/ Diagrams & Examples)" sciencing.com, https://www.sciencing.com/tension-physics-definition-formula-how-to-find-w-diagrams-examples-13720451/. 28 December 2020.
APA
Dusto, Amy. (2020, December 28). Tension (Physics): Definition, Formula, How To Find (W/ Diagrams & Examples). sciencing.com. Retrieved from https://www.sciencing.com/tension-physics-definition-formula-how-to-find-w-diagrams-examples-13720451/
Chicago
Dusto, Amy. Tension (Physics): Definition, Formula, How To Find (W/ Diagrams & Examples) last modified August 30, 2022. https://www.sciencing.com/tension-physics-definition-formula-how-to-find-w-diagrams-examples-13720451/