When you walk across your carpet on a cold winter's day, it doesn't feel cold to your feet. However, once you step onto the tile flooring in your bathroom, your feet feel instantly chilly. Are the two floors somehow different temperatures?

You certainly wouldn't expect them to be, given what you know about thermal equilibrium. So why do they feel so different? The reason has to do with thermal conductivity.

Heat is energy that transfers between two materials due to temperature differences. Heat flows from the object of higher temperature to the object of lower temperature until thermal equilibrium is achieved. Methods of heat transfer include thermal conduction, convection and radiation.

Thermal ​conduction​ is the mode discussed in more detail later in this article, but briefly it is heat transfer via direct contact. Essentially the molecules in the warmer object transfer their energy to the molecules in the cooler object via collisions until both objects are the same temperature.

In ​convection​, heat is transferred via motion. Imagine the air in your house on a cold winter day. Have you noticed that most heaters are usually located near the floor? As heaters warm the air, that air expands. When it expands, it becomes less dense, and so it rises above the cooler air. The cooler air is then near the heater, so the air can warm, expand and so on. This cycle creates convection currents and causes the heat energy to disperse through the air in the room by mixing the air as it is heated.

Atoms and molecules release electromagnetic ​radiation​, which is a form of energy that can travel through the vacuum of space. This is how the heat energy from a warm fire reaches you, and how the heat energy from the sun makes its way to Earth.

Thermal conductivity is a measure of how easily heat energy moves through a material or how well that material can transfer heat. How well heat conduction occurs depends on the thermal properties of the material.

Consider the tile floor in the example in the beginning. It is a better conductor than the carpet. You can tell just by feel. When your feet are on the tile floor, the heat leaves you much faster than it does when you are on the carpet. This is because the tile allows the heat from your feet to move through it much more quickly.

Just like specific heat capacity and latent heats, conductivity is a property specific to the material at hand,. It is denoted by the Greek letter κ (kappa) and is usually looked up in a table. The SI units of conductivity are watts/meter × Kelvin (W/mK).

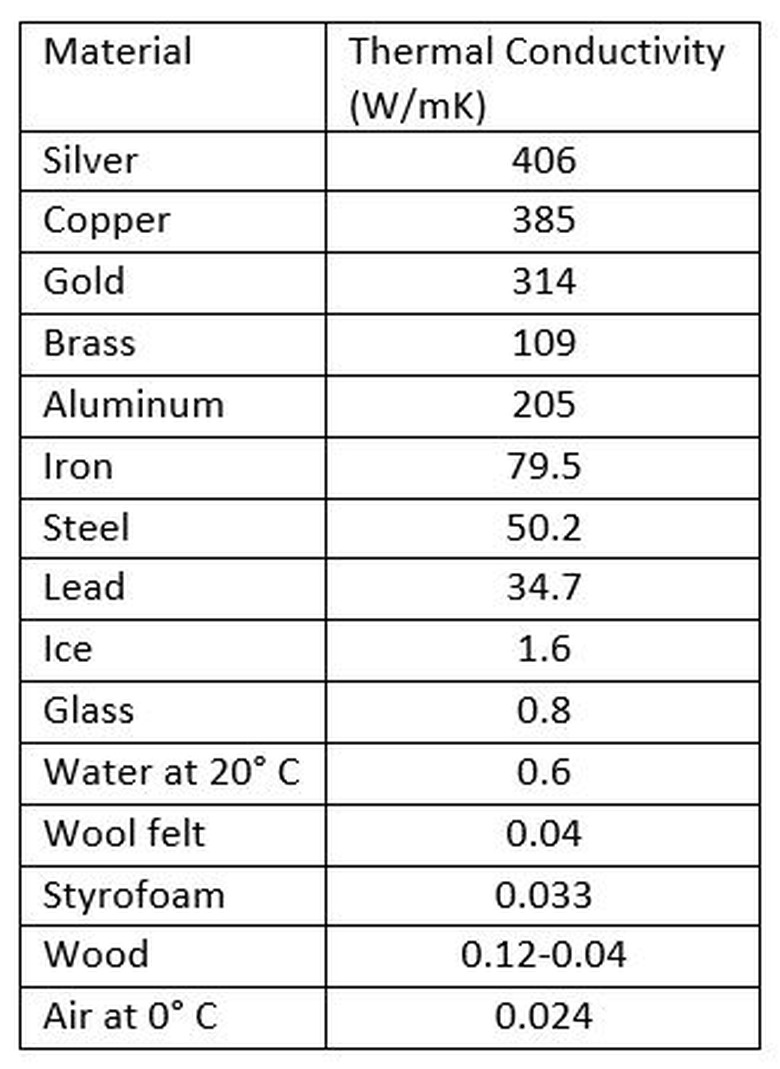
Objects with high thermal conductivity are good conductors while objects with low thermal conductivity are good insulators. A table of thermal conductivity values is given here.

As you can see, objects that often feel “cold” to the touch, such as metals, are good conductors. Note also how good of a thermal insulator air is. This is why big fluffy jackets keep you warm in winter: they trap a large layer of air around you. Styrofoam is also an excellent insulator, which is why it is used to keep food and drinks warm or cold.

As heat diffuses through the material, a temperature gradient exists across the material from the end closest to the heat source to the end farthest from it.

As heat moves through the material and before equilibrium is achieved, the end closest to the heat source will be the warmest, and the temperature will decrease linearly to its lowest level at the far end. As the material approaches equilibrium, however, this gradient flattens out.

How well heat can move though an object depends not only on that object's conductivity, but on the size and shape of the object as well. Imagine a long metal rod conducting heat from one end to the other. The amount of heat energy that can pass though per unit time will depend on the rod's length as well as how big around the rod is. This is where the notion of thermal conductance comes into play.

The thermal conductance of a material, such as an iron rod, is given by the formula:

where ​A​ is the cross-sectional area of the material, ​L​ is the length and κ is the thermal conductivity. The SI units of conductance are W/K (watts per Kelvin). This allows for an interpretation of κ as the thermal conductance of a unit area per unit thickness.

Conversely thermal resistance is given by:

This is simply the inverse of conductance. Resistance is a measure of how much opposition there is to the heat energy passing through. Thermal resistivity is likewise defined as 1/κ.

The rate at which heat energy ​Q​ moves through the length ​L​ of the material when the temperature difference between the ends is ​ΔT​ is given by the formula:

This can also be written as:

Note that this is directly analogous to what happens with current in electrical conduction. In electrical conduction, the current is equal to the voltage divided by the electrical resistance. Electrical conductivity and electrical current are analogous to thermal conductivity and current, voltage is analogous to temperature difference and electrical resistance is analogous to thermal resistance. All the same math applies.

​Example:​ A hemispherical igloo made of ice has an inner radius of 3 m and thickness of 0.4 m. Heat escapes the igloo at a rate that depends on the thermal conductivity of ice, κ = 1.6 W/mK. At what rate must thermal energy be continuously generated inside the igloo in order to maintain a temperature of 5 degrees Celsius inside the igloo when it is -30 C outside?

​Solution:​ The correct equation to use in this situation is the equation from before:

You are given κ, ​ΔT​ is just the difference in temperature range between inside and outside and ​L​ is the thickness of the ice. ​A​ is a little trickier. To find ​A​ you need to find the surface area of a hemisphere. This would be half the surface area of a sphere, which is 4π​r​². For ​r​, you can choose the average radius (the radius of the inside of the igloo + half the thickness of the ice = 3.2 m), so the area is then:

Plugging everything into the equation then gives:

​Application:​ A heat sink is a device that transfers heat from objects at high temperatures to the air or to a liquid that then carries the excess heat energy away. Most computers have a heat sink attached to the CPU.

The heat sink is made of metal, which conducts the heat away from the CPU, and then a small fan circulates air around the heat sink, causing the heat energy to disperse. If done right, the heat sink allows the CPU to operate at a steady state. How well the heat sink works depends on the conductivity of the metal, the surface area, the thickness and the temperature gradient that can be maintained.