Torque, which rhymes with "fork," is the angular analog of force. It is sometimes called a twisting force or a ​torsional​ force.

When you push a box horizontally along a surface at constant speed, you are exerting a "traditional" mechanical force on the box. But when you apply a turn to a wrench, the variables are immediately different because the force you are applying to move something is being indirectly applied – processed, if you will, through the act of turning and the physical laws governing this kind of motion.

• One important thing to be aware of up front: While torque can be thought of as a force in terms how it affects objects, it actually has units of work, or force times distance. ​However, torque is a vector quantity.​

A net torque (which you can think of as "total torque," as it's the vector sum of the torques in a system) causes a change in an object's angular velocity, just like a net force effects a change in an object's linear velocity.

A net torque is required to open a door or a pickle jar, to make a seesaw move, or to loosen the lug nut on a tire, among other things. Conveniently, the math and equations involved in rotational motion are analogous to those used for linear motion, so kinematic problems involving torque can be solved in the same general way as long as you keep track of your variables and signs properly.

The basic quantities of interest in equations of motion are displacement, velocity (the rate of change of displacement), acceleration (the rate of change of velocity) and time ​t​ itself. Mass does not enter these equations, but it is incorporated into mechanical energy (kinetic plus potential energy) as well as momentum (mass times velocity).

Angular velocity ​ω​ is the rate of change of the angle ​θ​ (usually in radians per second or rad/s, expressed as s^-1) with respect to a fixed reference point, analogous to linear velocity ​v​. Accordingly, angular acceleration ​α​ is the rate of change of ​ω​ with respect to time. Linear momentum ​p​ is expressed as ​m​v​​, whereas angular momentum ​L​ is the product of ​I​ (moment of inertia, incorporating both mass and its distribution in objects of different shapes) and ​ω​:

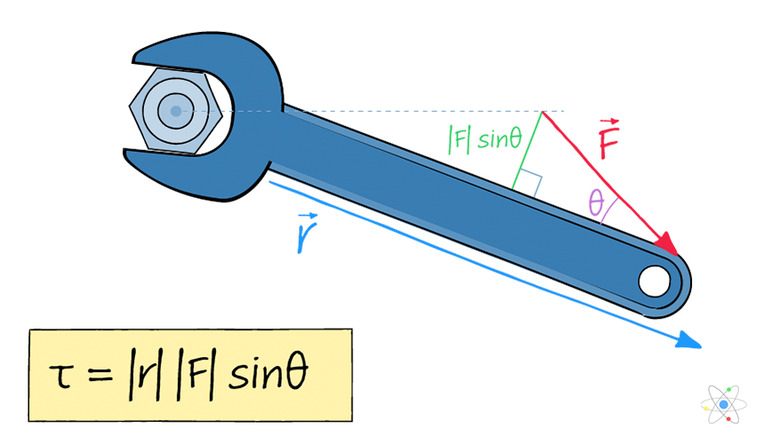
Whereas in linear (translational) kinematics, the general equation of interest is ​F_net​ = m​a​ (Newton's second law), the analogous relationship with torque is that net torque equals the moment of inertia times the angular acceleration. Individual torques can be found via the following expression:

τ = r × F ​= |​r||F|sin θ

The "τ" representing torque is the the Greek letter ​tau​. (Without a Greek alphabet, physicists would have been left scratching their heads for symbols to use in equations way back in Newton's time in the 1700s.) Also, ​r​ is the radius in meters in SI units, also called the lever arm; because it also has a direction, it is a vector quantity. Force, as is almost always the case, is in newtons (N).

The "×" here implies a special kind of multiplication between vectors, as torque is the ​cross product​ of radius and force. The direction of the torque vector is perpendicular to the plane formed by the direction of the force vector and the direction of the lever arm, which have an angle ​θ​ between them.

Often the force acts by design in a direction perpendicular to the lever arm; this makes intuitive sense, but is borne out by the math since sin θ has is maximum value of 1 at θ = 90 degrees (or π/2).

The lever arm ​r​ (also called a ​moment arm​) is the displacement from the axis of rotation to the point at which the force is applied. In some problems, this force placement is not obvious without a close look at a diagram, because it can be between the axis of rotation and the load being moved.

The direction of net torque is along the axis of rotation with direction determined by the ​right-hand rule​: If you curl the fingers if your right hand from the direction of ​r​ to the direction of ​F​, your thumb points in the direction of the torque vector.

• Torque points in the same direction as angular acceleration(when it is sufficient to effect a change in rotational motion of the object in question).

1. You apply a force of 100 N perpendicularly to a wrench 10 cm (0.1 m) from the middle of a stuck bolt. What is the net torque?

You apply the same force of 100 N perpendicularly to the end of this (very long) wrench, 1 m from the middle of the stubborn bolt. What is the new net torque?

2. Suppose you are exerting a clockwise force of 50 N on a horizontal wheel 3 m from its axis of rotation. A friend is pushing with a force of 25 N in a counterclockwise direction 5 m from the axis of rotation. In what direction will the wheel move?

Because the magnitude of "your" torques (50 times 3 or 150 newton-meters) exceeds that of your friend (25 times 5 or 125 newton-meters), the wheel will move clockwise, as the net torque is 150 – 125 = 25 newton-meters in that direction.

When all of the torques on an object are balanced (that is, they mathematically and functionally cancel each other out), an object is said to be in ​rotational equilibrium​. As with linear force and Newton's second law, when the net force is zero, the object's velocity doesn't change (but can be nonzero). In the case of rotational motion, that means its rotational velocity doesn't change.

Consider a balanced see-saw. Obviously, two children of equal mass placed at equal distances from the center will not make it move. But two kids of ​different​ masses ​can​ balance it, too; they just must be at different distances.

• Note that the force the kids sitting on the seesaw are "applying" is the force of gravity, or their weight. However, they still have to work their brains to fix this "problem"!

Only the component of an applied force that is at a right angle at distance ​r​ from the axis of rotation contributes to the net torque on an object. This means that a very strong person trying to rotate an object by applying a force at a small angle will have a harder time getting it to begin rotating than someone of modest strength will by applying the force perpendicularly since sin θ = 0 at θ = 0, and sin θ approaches 1 as θ approaches 90 degrees.

Many physics problems have angles that crop up repeatedly because they are trigonometrically convenient as well as representative of real-life problems. Thus if you see that a force is applied at a lesser angle, like 45 or 30 degrees, you will become accustomed to knowing the values of the sines and cosines of these angles by heart before long.

Thus, the most efficient way to use a wrench in physics lingo – that is, how to get the most net torque out of your applied force – is to apply that force at 90 degrees. But you can probably imagine, or even recall, situations in which this isn't feasible because of space limitations in accessing a bolt or the like.