An intrepid backpacker might look at the map and determine she needs to travel 10 more kilometers "north-northwest." She could march in a straight line directly to her destination, but she could also hike for a while west, then for a longer while north and still get there in the end.

If she takes the scenic route, she will have broken down her direct trip into north and west ​components​. Knowing the details of each component will in turn allow her to calculate the total distance and displacement she traveled, her average speed and other stats about the trip. Stats a physicist would find interesting.

Components is another word for "parts" – so the short definition of vector components is "vector parts."

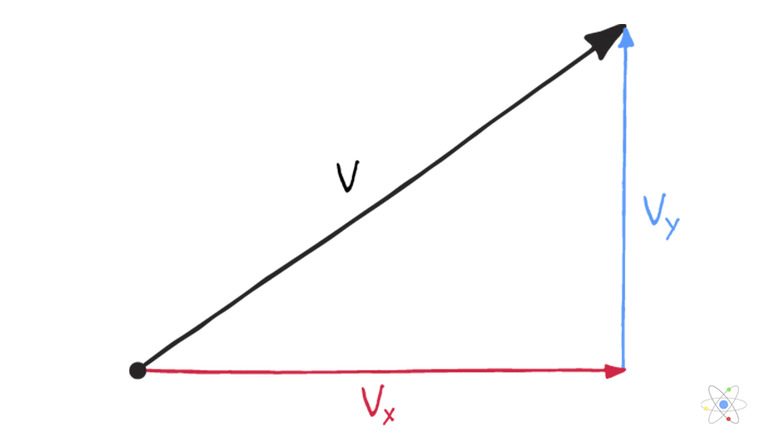
Vector components come into play when considering directions that are not either perfectly vertical or horizontal. In these cases, a diagonal vector describes motion that is two dimensional: somewhat ​vertical and horizontal​. The magnitude of the vector would be given by the length of the diagonal line, and the direction of the vector would be given by a direction angle.

On the coordinate system, a vector directed parallel to either the positive x-axis or y-axis is simple to quantify: Simply count up the distance it covers to find its magnitude. Its angle is then either 0 or 90 degrees (or a multiple thereof, depending how the vector is drawn).

For a diagonal vector however, finding the magnitude can be tricky, until you draw some right triangles.

Consider driving a car three blocks west and then four blocks south. You can find the total distance traveled by adding up the blocks covered (in this case, seven blocks), but the total displacement follows a diagonal path from starting to ending point.

Without knowing the angle, the length of the hypotenuse in the right triangle showing the car's path (the magnitude of its displacement vector) can be found using the Pythagorean Theorem:

In the example above, the car drove in two directions that are ​orthogonal​, or that are at 90 degrees to one another. Therefore, one direction can be aligned to the x-axis and one can be aligned to the y-axis, becoming the ​x-component​ and ​y-component​ of the vector showing the car's displacement, respectively. These are sometimes called the horizontal and vertical components of the vector quantity.

Any time horizontal and vertical components of a vector are given, they can be aligned "tip to tail" as is done in vector addition (referring to the ends of the arrows for the vectors) to build a right triangle.

The hypotenuse of the right triangle always forms the ​resultant​ vector.

This method ​works only if the​ ​vector components​ ​are aligned correctly so that the tip of one (the arrowhead) connects with the tail of the other​ in the given directions. Additionally, as with any addition, only vectors with the same units can be added this way.

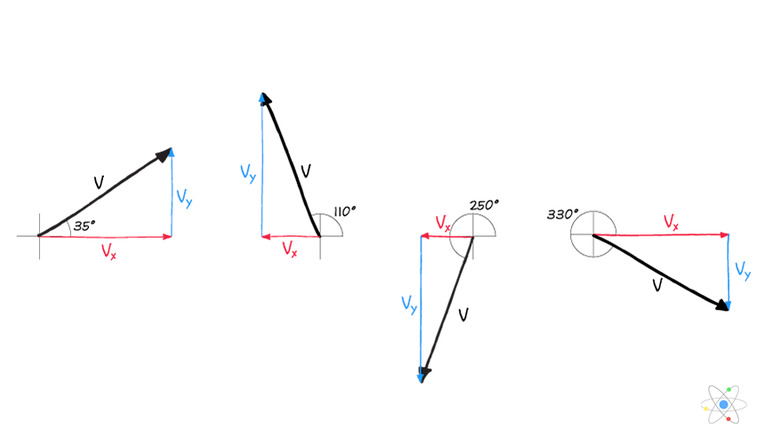
But what if the x- and y-components are unknown to begin with? For instance, what if only the fact that the car moved five blocks southwest at 53 degrees is given?

Starting with a diagonal vector's magnitude and angle of direction and then breaking it down into how much of that magnitude is directed along the x- or y-axis is known as ​resolving the​ ​components of a vector​.

The first step is to draw a right triangle where the given vector and its angle form one corner. The x-component relates to the hypotenuse using a cosine function, and the y-axis relates using a sine function.

Memorizing this is not deep learning. Nonetheless, here are those relationships written out:

• x-component (adjacent side) = hypotenuse × cos(angle)
• y-component  (opposite side)= hypotenuse × sin(angle)

Because vector components add together to form the resultant vector, they are typically notated using subscripts ​x​ and ​y​, for x-component and y-component, respectively.

If the velocity v of a duck flying in the air at 20 degrees with respect to the horizontal is 5 m/s, then:

• vx = 5cos(20) = 4.7 m/s 
• vy = 5sin(20) = 1.7 m/s. 

The duck is covering more ground horizontally than vertically each second.