Work (Physics): Definition, Formula, How To Calculate (W/ Diagram & Examples)
Physics, in addition to being a word that unfortunately scares off potential future science buffs in advance, is at its core the study of how objects move. This includes everything from entire clusters of galaxies to particles almost too small to imagine, much less properly visualize.
And a huge part of applied physics (that is, the branch of physical science concerned with putting knowledge to use rather than "merely" theorizing) is figuring out how to get more work out of less energy.
Work, in addition to being a near-daily obligation for employees and students as well as a general signifier of effort well spent, is one of a number of vital formal quantities in physics that has units of energy. In short, whenever energy is used to make an object move, work is being done on that object.
Everyday examples of work being done include elevators carrying hotel guests up to their floors, a child pulling a sled up a hill or the expansion of gas in a combustion engine driving a piston. To properly understand this concept, it's helpful to review some of the basics about energy, motion and matter that make "work" a viable concept in physical science in the first place.
The Definition of Work
The Definition of Work
Work the physical result of a force applied over some distance, as the force produces a displacement of the object on which it acts. Work has a positive value when the force is in the same direction as the motion and a negative value when it is in the opposite direction (that "negative work" can even happen probably seems strange, but you'll see how momentarily). Any system that possesses energy is capable of doing work.
When an object doesn't move, no work is done on it. This is true no matter how much effort is put into a task, like trying to move a large boulder yourself. In this case, the energy from your muscle contractions is lost as heat dissipated from those muscles. So, though you do no work in this scenario, at least you get in a workout of sorts.
Only the component of a force directed in line with the object's displacement contributes to the work done on it. If someone is walking in a direction corresponding to the positive x-axis on a typical coordinate system and experiences a force from her left whose vector is almost perpendicular to her movement but points very slightly in the x-direction, only that comparatively tiny x-component of the force factors into the problem.
When you walk down a flight of stairs, you are doing work to prevent yourself from moving even faster (free-falling), but because your motion is still in the direction opposing your efforts, this is an example of work with a negative sign. The combined net work done on you by gravity and yourself is positive, but a smaller positive number than it would be without your "working" in direct opposition.
Work Has Units of Energy
Work Has Units of Energy
The total energy of a system is its internal or thermal energy plus its mechanical energy. Mechanical energy can be divided into energy of motion (kinetic energy) and "stored" energy (potential energy). The total mechanical energy in any system is the sum of its potential and kinetic energies, each of which can take various forms.
Kinetic energy is energy of motion through space, both linear and rotational. If a mass m is held a distance h above the ground, its potential energy is mgh. Where the acceleration due to gravity, g, has the value of 9.80 m/s2 near Earth's surface.
If the object is released from rest at height h and allowed to fall downward to Earth (h = 0), its kinetic energy at impact is (1/2)m**v2** = mgh, as all of the energy has been converted from potential to kinetic during the fall (assuming no frictional or heat energy losses). At all times, the sum of the potential energy of the particle and its kinetic energy remains constant.
- Because force has units of newtons (kg⋅m/s2) in the SI (metric) system and distance is in meters, work and energy in general have units of kg⋅m2/s2. This SI unit of work is known as the Joule.
The Formula for Work
The Formula for Work
The standard equation for work is:
\(W=F\cdot d\)
where d is displacement. Though force and displacement are both vector quantities, their product is a scalar product (also called a dot product). This curiosity is true of other vector quantities that are multiplied together, such as force and velocity, the multiplication of which results in the scalar quantity power. In other physical situations, the multiplication of vectors produces a vector quantity, known as a cross-product.
The individual forces in a system **F1, F2, F3 **... **Fn** do work with magnitudes equal to **F1****d1, F2**d**2**, and so on; these individual products, which can include negative as well as positive values, can be summed to give the system's total work, or net work. The formula for the net work Wnet done on an object by a net force Fnet is
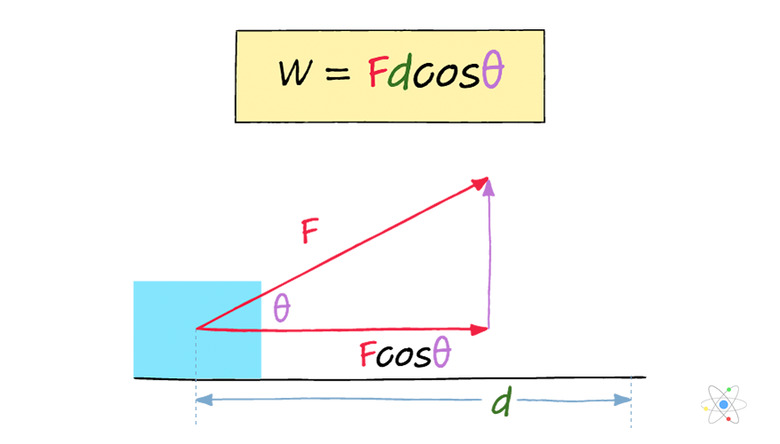
\(W_{net}=F_{net}\cdot d=F_{net}d\cos{\theta}\)
where θ is the angle between the direction of motion and the applied force. You can see that for values of θ for which the cosine of the angle is 0, such as when the force is perpendicular to the direction of motion, no net work is done. Also, when the net force acts opposite the direction of motion, the cosine function gives a negative value, producing the aforementioned "negative work" as a result.
How to Calculate Work
How to Calculate Work
You can calculate total work by adding up the amount of work done by different forces in a problem. In all cases, calculating work requires a complete understanding of the vectors in the problem, not merely the numbers that go with them. You will need to put basic trigonometry to use.
- **Note:** In real life, when a force acts on an object besides gravity, it is unlikely to be constant. Any force F you see mentioned in these examples can be assumed to be a constant force. When forces vary, the relationships noted here remain valid, but you will need to perform integral calculus to solve the associated problems.
**Example:** A dog pulling a 20-kg child-sled combination across a horizontal snowfield accelerates from rest to a velocity of 5 m/s over the course of 5 seconds (a = 1 m/s2). How much work does the dog do on the child-sled combination? Assume friction is negligible.
First, you calculate total force applied by the dog to the child and sled: F = ma = (20 kg)(1 m/s2) = 20 N. Displacement is average velocity (v – v0)/2 (= 5/2) multiplied by time t (= 5 s), which is 12.5 m. Thus total work is (20 N)(12.5 m) = 250 J.
- How would you solve this problem using the work-energy theorem instead?
Work for Force at an Angle
Work for Force at an Angle
When force is not applied at 0 degrees (i.e., if it is at an angle to the object), use simple trigonometry to find the work done on that object. You need only know how to use cosine and sine for introductory-level problems.
For example, imagine the dog in the above situation standing on the edge of a cliff, so that the rope between the child and the dog makes an angle of 45 degrees with the horizontal snowfield. If the dog applies the same force as before at this new angle, you find that the horizontal component of this force is given (cos 45°)(20 N) = 14.1 N, and that the resulting work done on the sled is (14.1 N)(12.5 m) = 176.8 J. The new acceleration of the child is given by the value of the force and Newton's law, F = ma: (14.1 N)/20 kg) = 0.71 m/s2.
The Work-Energy Theorem
The Work-Energy Theorem
It is the work-energy theorem that formally grants work the "privilege" of being expressed in terms of energy. According to the work-energy theorem, the net work done on an object is equal to the change in kinetic energy:
\(W_{net}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\)
where m is the object's mass and **v0** and v are its initial and final velocities.
This relationship comes in very handy in problems involving work, force and velocity where the magnitude of the force or some other variable is unknown, but you have or can calculate the rest of what you need to proceed toward a solution. It also underscores the fact that no net work is done at constant speed.
Rotational Work
Rotational Work
The work-energy theorem, or work-energy principle, takes on a recognizable, but slightly different form for objects rotating about a fixed axis:
\(W_{net}=\frac{1}{2}I\omega_f^2-\frac{1}{2}I\omega_i^2\)
Here ω is angular velocity in radians per second (or degrees per second) and I is a quantity analogous to mass in linear motion called the moment of inertia (or the second moment of area). It is specific to the shape of the rotating object and depends also on the axis of rotation. Calculations are done in the same general way as for linear motion.
What Are Newton’s Laws of Motion?
What Are Newton's Laws of Motion?
Isaac Newton, one of the leading mathematical and scientific minds of the Scientific Revolution, proposed three laws governing the behavior of moving objects.
- Newton's first law of motion states that an object in motion with constant velocity will remain in that state unless acted on by an unbalanced external force. An important consequence of this law of inertia is that net force is not required to maintain even the highest velocity provided that velocity doesn't change.
- Newton's second law of motion states that net forces act to change the velocity of, or accelerate, masses: **Fnet** = ma. Force and acceleration are vector quantities and have both magnitude and direction (x-, y- and z-components, or angular coordinates); mass is a scalar quantity and possesses magnitude only. Work, like all forms of energy, is a scalar quantity.
- Newton's third law of motion states that for every force in nature there exists a force equal in magnitude but opposite in direction. That is, for every F there exists a force -F within the same system, whether the system is one you have defined with your own boundaries or is simply the cosmos as a whole.
Newton's second law relates directly to the law of conservation of energy, which asserts that the total energy in a system (potential plus kinetic) remains constant, with energy being transferred from one form to another but never being "destroyed" or produced out of nothing.
Cite This Article
MLA
Beck, Kevin. "Work (Physics): Definition, Formula, How To Calculate (W/ Diagram & Examples)" sciencing.com, https://www.sciencing.com/work-physics-definition-formula-how-to-calculate-w-diagram-examples-13720810/. 28 December 2020.
APA
Beck, Kevin. (2020, December 28). Work (Physics): Definition, Formula, How To Calculate (W/ Diagram & Examples). sciencing.com. Retrieved from https://www.sciencing.com/work-physics-definition-formula-how-to-calculate-w-diagram-examples-13720810/
Chicago
Beck, Kevin. Work (Physics): Definition, Formula, How To Calculate (W/ Diagram & Examples) last modified August 30, 2022. https://www.sciencing.com/work-physics-definition-formula-how-to-calculate-w-diagram-examples-13720810/