How To Write The Equation Of A Linear Function Whose Graph Has A Line That Has A Slope Of (-5/6) And Passes Through The Point (4,-8)

The equation for a line is of the form y=mx+b, where m represents the slope and b represents the intersection of the line with the the y-axis. This article will show by an example how we can write an equation for the line that has a given slope and passes through a given point.

Step 1

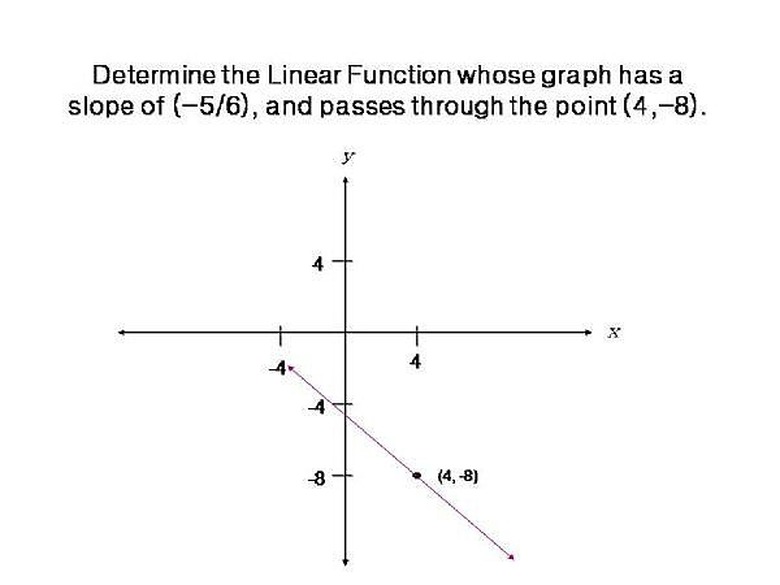
We will find the Linear Function whose graph has a slope of (-5/6), and passes through the point (4,-8). Please click on the image to see the graph.

Step 2

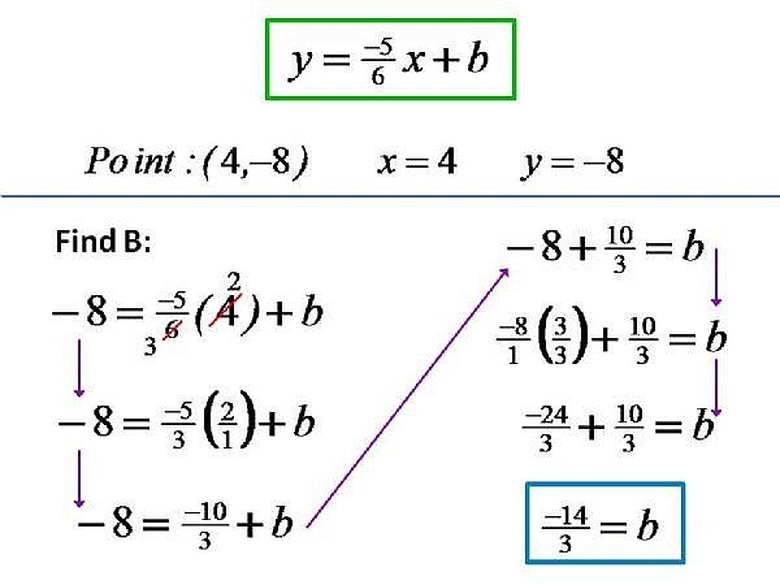
In order to find the Linear Function, we will use the Slope-Intercept form, which is y=mx+b. M is the slope of the line, and b is the y-intercept. We already have the slope of the line, (-5/6), and so we will replace m with the slope. y=(-5/6)x+b. Please click on the image for a better understanding.

Step 3

Now, we can replace x and y with the values from the point that the line goes through, (4,-8). When we replace x with 4 and y with -8, we get -8=(-5/6)(4)+b. By simplifying the expression, we get -8=(-5/3)(2)+b. When we multiply (-5/3) by 2, we get (-10/3). -8=(-10/3)+b. We will add (10/3) to both sides of the equation, and by combining like terms, we get: -8+(10/3)=b. In order to add -8 and (10/3), we need to give -8 a denominator of 3. To do this, we mulitply -8 by (3/3), which equals -24/3. We now have (-24/3)+(10/3)=b, which is equal to (-14/3)=b. Please click on the image for a better understanding.

Step 4

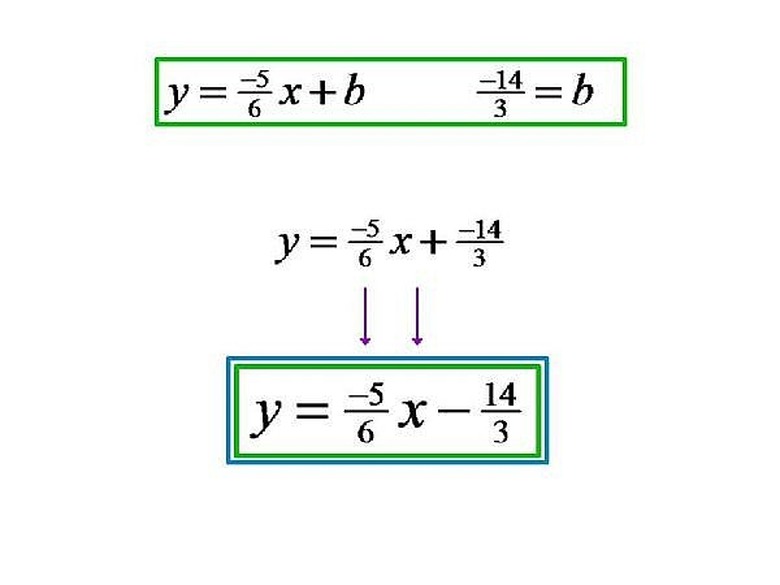
Now that we have the value for b, we can write the Linear Function. When we replace m with (-5/6) and b with (-14/3) we get: y=(-5/6)x+(-14/3), which is equal to y=(-5/6)x-(14/3). Please click on the image for a better understanding.