If you've been following Sciencing's March Madness coverage, you know that statistics and numbers play a huge role in the NCAA Tournament.

The best part? You don't have to be a sports fanatic to work on some sports-centric math problems.

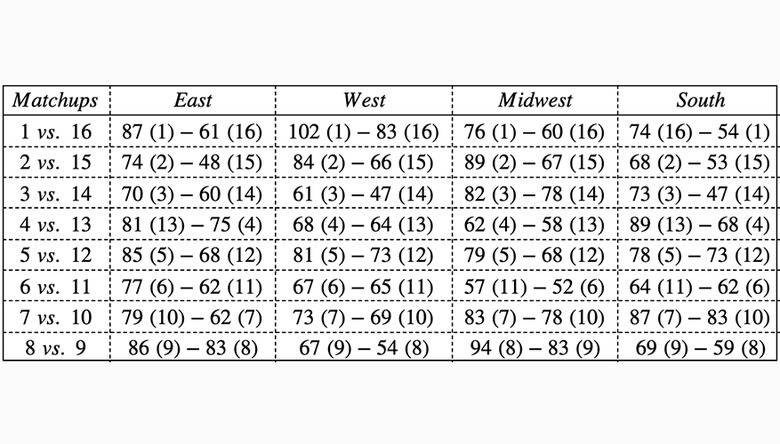
We've created a series of math questions that incorporate data from last year's March Madness results. The table below shows results of each Round of 64 seeding matchup. Use it to answer questions 1-5.

If you don't want to see the answers, head back to the original sheet.

Good luck!

Check out our articles on mean, median, mode and interquartile range if you need to brush up before getting started.

Question 1: What is the mean difference of scores in East, West, Midwest and South Region for 2018 March Madness Round of 64?

Question 2: What is median difference of scores in East, West, Midwest and South Region for 2018 March Madness Round of 64?

Question 3: What is IQR (Interquartile Range) of difference of scores in East, West, Midwest and South Region for 2018 March Madness Round of 64?

Question 4: Which matchups were outliers in terms of the difference of scores?

Question 5: Which region was more "competitive" in the 2018 March Madness Round of 64? Which metric would you use to answer this question: Mean or Median? Why?

Competitiveness: The smaller the difference between winning and losing score, the more "competitive" the game is. For example: If the final scores of two games were 80-70 and 65-60 then according to our definition the latter game was more “competitive.”

Question 1 (difference of scores):

East: 26, 26, 10, 6, 17, 15, 17, 3
West: 19, 18, 14, 4, 8, 2, 4, 13
Midwest: 16, 22, 4, 4, 11, 5, 5, 11
South: 20, 15, 26, 21, 5, 2, 4, 10

Question 2 (mean of difference of scores):

Mean = Sum of all observations/Number of observations
East: (26+26+10+6+17+15+17+3)/8 = 15
West: (19+18+14+4+8+2+4+13)/8 = 10.25
Midwest: (16+22+4+4+11+5+5+11)/8 = 9.75
South: (20+15+26+21+5+2+4+10)/8 = 12.875

Question 2 (median of difference of scores):

Median is the 50th percentile value.

The median of a list can be found by arranging the numbers in increasing order and then picking the middle value. Here since the number of values is a even number (8), so the median will be mean of the two middle values, in this case mean of 4th and 5th value.

East: Mean of 15 and 17 = 16
West: Mean of 8 and 13 = 10.5
Midwest: Mean of 5 and 11 = 8
South: Mean of 10 and 15 = 12.5

Question 3 (IQR of difference of scores):

IQR is defined as the difference between 75th percentile (Q3) and 25th percentile value (Q1).

Question 4 (outlier matchups):

Outliers: Any value that is either less than Q1 - 1.5 x IQR or greater than Q3 + 1.5 x IQR

No, outliers in the data.

Question 5 (most competitive region):

Order of competitiveness using mean: Midwest > West > South > East
Order of competitiveness using median: Midwest > West > South > East

Since in this particular case there are no outliers either metric works. But the students should talk about the effect of outliers on mean of observations.

Check out our article on binomial probability if you need a refresher.

Free Throw: In basketball, free throws or foul shots are unopposed attempts to score points by shooting from behind the free throw line.

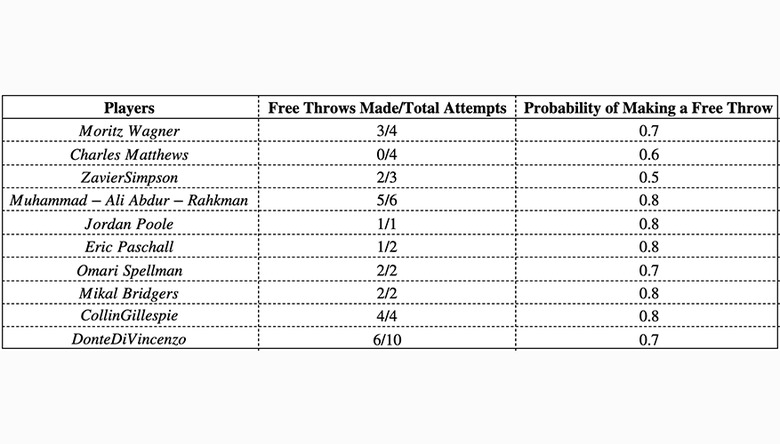
Assuming that each free throw is an independent event then calculating success in free throw shooting can be modeled by Binomial Probability Distribution. Here's the data for free throws made by players in the 2018 National Championship game and their probability of hitting the free throw for the 2017-18 season (note the numbers have been rounded to closest one-place decimal number).

Question 1: Calculate the probability for each player getting the given number of successful free throws in the number of attempts they took.

Answer:

Binomial Probability Distribution:

Here's a look at the answer on a table:

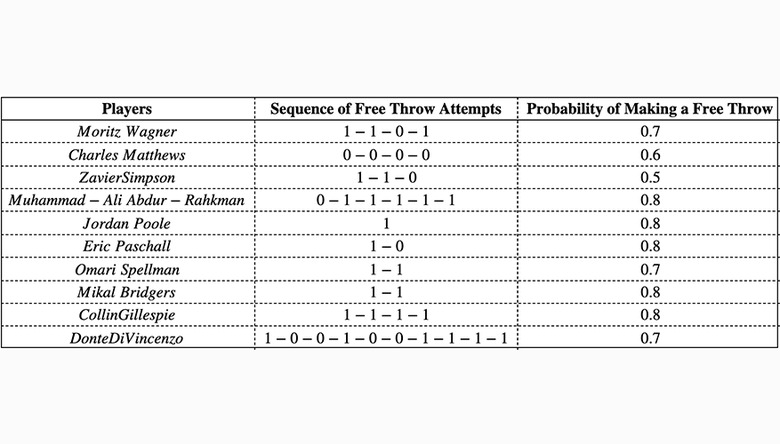
Question 2: Here's the sequence data for the players' free throw shooting in the same game. 1 means that the free throw was successful and 0 means that it was unsuccessful.

Calculate the probability for each player hitting the exact sequence above. Is the probability different from what was calculated before? Why?

Answer:

The probabilities can be different since in the previous question we didn’t care about the order in which the free throws were made. But the probability will be same for the cases where there’s only one possible ordering. For example:

Charles Matthews was unable to score a free throw on all 4 attempts and Collin Gillespie was successful on all 4 attempts.

Using the above probability numbers, answer these questions:

1. Which players had an unlucky/bad day with their free throw shooting?
2. Which players had a lucky/good day with their free throw shooting?

Answer: Charles Matthews had unlucky day at free throw line since the probability of him missing all his free throws was 0.0256 (there was only 2.5 percent chance of that event occurring).

Feeling the March Madness spirit? Check out our tips and tricks for filling out a bracket, and read why it's so tough to predict upsets and pick a perfect bracket.